Sizing up ACA risk adjustment volatility: How the interplay between risk adjustment and issuer size influences profitability under the ACA
As commercial health plans evaluate financial results from the initial years of their Patient Protection and Affordable Care Act (ACA) experience, concerns have surfaced regarding the level of marketplace volatility—particularly for insurers with low membership. Over time, the focus of the perceived instability has shifted away from the (temporary) risk corridor program and has centered on the (permanent) risk adjustment program.
Recent studies1, 2, 3, including one commissioned by the Centers for Medicare and Medicaid Services (CMS)4, have furthered the discussion by analyzing the effects of actual 2014 risk transfers. Some of the reported conclusions share common themes. First, risk adjustment, despite some imperfections, did redistribute funds from plans with lower-risk enrollees to plans with higher-risk enrollees for all issuer sizes. Second, any adverse financial results experienced in 2014 may have been largely associated with mispricing, exacerbated by lack of risk corridor funding—not necessarily the risk adjustment program. Third, there appears to be an inverse relationship between issuer size and the variability of transfers in 2014.
Looking beyond the early results highlighted in these studies, we pursue an alternative approach to investigating the implications behind the risk adjustment program mechanics. Attempting to understand actual risk transfer results from 2014 is certainly a worthwhile pursuit; however, those outcomes represent just one data point and only from the inaugural year of the ACA. In this study, we set out to explain how risk adjustment might influence profitability patterns in a more typical year and whether those patterns change with the size of a health plan. What we discovered is a paradigm that does not seem to meaningfully reduce the volatility of financial outcomes and may not have the pinpoint accuracy needed to adequately compensate all plans for the risks they are prohibited from pricing into their premium rates.
We also explore the consequences of some mainstream proposals to modify risk adjustment long term, recognizing some of these ideas may be directly in reaction to the early 2014 results. Our modeling suggests:
- A cap on a health plan’s risk transfer payment can serve to limit profit instability for small issuers. However, several items would need to be addressed before any possible implementation, including the potential volatility in the value of the cap, the size of the cap relative to the risk transfer pool, the increased incentive for plans to attract healthy enrollees, and the funding mechanism.
- Pooling high-cost enrollees and spreading their costs may not meaningfully affect financial volatility.
- Although it is unclear how an issuer’s total profitability would be impacted, applying risk adjustment at a regional level could reduce profit volatility for regional plans, likely at the expense of increased volatility for statewide plans. Additional research is required to appreciate all market interactions and to address the regulatory challenges presented by such a change.
- The introduction of pharmacy data into the risk-scoring algorithm may improve the program’s accuracy, though it is uncertain if financial volatility will diminish or just manifest itself differently.
- Accounting for partial year enrollment in the risk adjustment program will likely level the playing field for new or growing health plans. Further modeling is necessary to isolate the extent of the impact.
Regardless of whether plans were priced appropriately in 2014, we approach the impacts of the risk adjustment program in this paper through a statistical lens. Doing so provides insights into where the market may head (rather than where it has been) as issuers presumably begin to rate more accurately for market risk.
Risk adjustment does not materially reduce aggregate profit volatility, regardless of issuer size
We simulate a 2017 individual medical insurance market in a theoretical state covering 250,000 total members. We distribute these members across eight health plans with various levels of market share (measured in lives) and perform 10,000 market-wide simulations, each time randomly reassigning enrollees to one of eight issuers.
We assume issuers have perfect knowledge of each member’s future claim costs and risk profile but do not know in advance which members they will enroll. This forces all carriers to price to market averages and creates a consistency among the premium rates. Accordingly, all simulations represent random outcomes that are not influenced by pricing biases. We assume issuers at or below 5% market share (12,500 lives) “purchase” commercial reinsurance with an annual $300,000 stop-loss deductible per member. By mitigating random catastrophic events, we more accurately represent the current insurance environment for small health plans. The resulting increase in administrative expenses for these plans reduces their priced-for profit by an average of about one percentage point.
The graph in Figure 1 displays the simulated distribution of pre-tax profit excluding risk transfers for several of the modeled issuers. We remove several issuers from the displayed outputs given consistency in the patterns relative to those shown. The graph in Figure 2 displays the variation of pre-tax profit including risk transfers. Each figure contains a table at the bottom highlighting key profitability measures. All risk adjustment calculations utilize the finalized 2017 coefficient set.
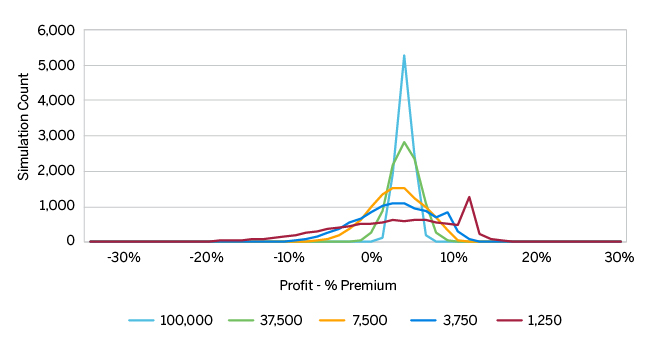
| Pretax Profit Statistics, Excluding Risk Adjustment | |||||
| Issuer Size | 100,000 | 37,500 | 7,500 | 3,750 | 1,250 |
| Average | 3.01% | 3.00% | 2.01% | 1.91% | 1.63% |
| Probability of Positive Margin | 100.0% | 95.0% | 73.0% | 67.2% | 61.1% |
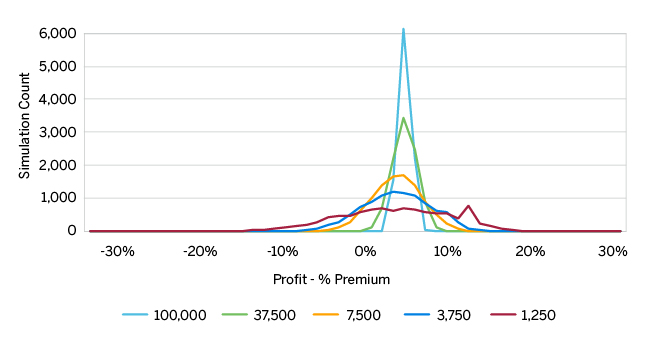
| Pretax Profit Statistics, Excluding Risk Adjustment | |||||
| Issuer Size | 100,000 | 37,500 | 7,500 | 3,750 | 1,250 |
| Average | 3.00% | 3.00% | 2.07% | 2.02% | 1.77% |
| Probability of Positive Margin | 100.0% | 97.5% | 75.1% | 68.3% | 60.3% |
Both figures illustrate the relationship between profit dispersion and the plan size—the smaller the plan, the more expansive the range of results. The frequency “spike” around 12% profit for the 1,250-life issuer and the similar, but muted, “plateau” near 9% for the 3,750-life issuer reflect suppression of the positive profit tail from medical loss ratio (MLR) rebates. Refer to the Methodology section for further details regarding rebates.
Comparing the numbers in more detail, total profit variability compresses slightly after introducing risk adjustment, but the distribution of profit remains effectively unchanged. In fact, the expected average profit for six out of the eight modeled issuer sizes changes by 0.06% or less of premium, and the probability of posting a loss for the smallest issuer increases less than one percentage point. The smallest issuer remains profitable in just over 60% of simulations, both before and after risk transfers. We include summary statistics underlying the graphs and additional profitability metrics in Figure 8 and Figure 9, respectively, in the Appendix.
In our “perfectly priced” and undifferentiated marketplace, risk adjustment does not overtly address volatility for any size issuer and does not offer material protection against loss for small issuers. If a health plan had any preconceived belief that risk adjustment would mitigate the deviation of profit outcomes, the information displayed in Figures 1 and 2 would suggest otherwise. The key to understanding the similarity of the modeled profit patterns by issuer before and after risk adjustment is to dig “behind the averages” and track each simulated event individually, which we do next.
Risk transfers are inaccurate predictors of claim costs, which more meaningfully impacts small issuers
Taken together, Figures 1 and 2 above imply the pattern of average profit is reasonably stable after applying risk transfers—contracting somewhat but generally not rewriting the volatility story. However, it turns out profitability levels reshuffle considerably among the individual simulations, as issuers bear different levels of risk and are compensated in different amounts.
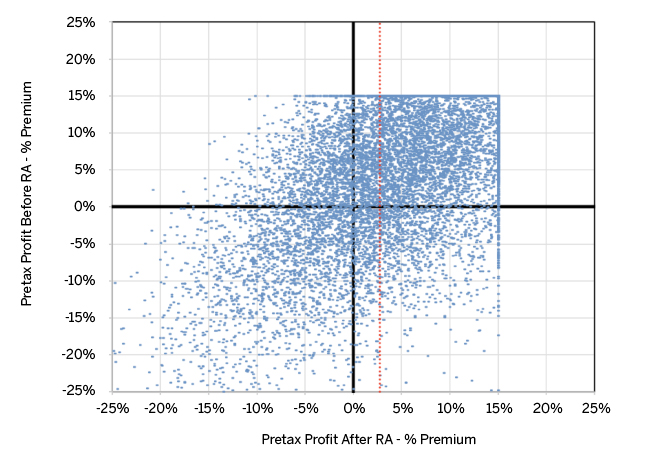
The graph in Figure 3 displays pretax profit before and after risk transfers for the 1,250-life issuer for all 10,000 simulations.
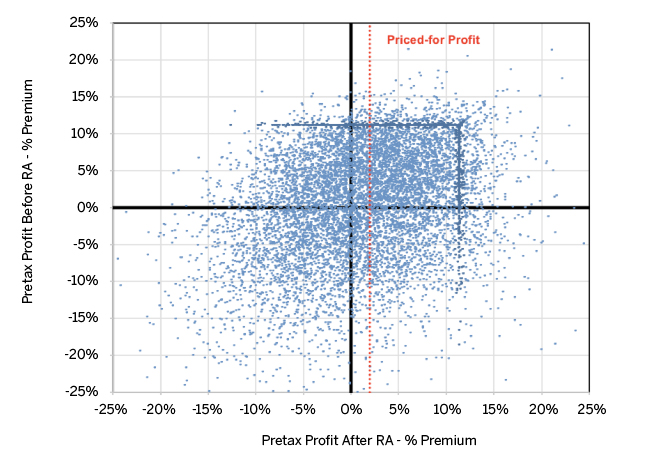
The position on the vertical axis represents pretax profit before risk adjustment, while the position on the horizontal axis represents pretax profit after risk adjustment. For example, all points on the horizontal line at -10% represents pre-risk adjustment losses of 10% of premium. Moving from left to right, the amount of risk transfer compensation increases, contributing to rising profitability and vice versa. The red dashed bar located at 2% profit marks the small carrier’s approximate pricing target. The more effectively risk adjustment redistributes funds based on risk, the more compressed the simulated values will be around the vertical red bar at 2% profit. The “lines” formed from clusters of simulations near the 12% profit levels are the result of compression after MLR rebating, analogous to the frequency “spikes” in Figures 1 and 2.
Figure 3 highlights both the imprecision of transfers as risk compensation and the potential magnitude of the swing in profit from pre- to post-risk adjustment. Keep in mind these outcomes occur even with perfect knowledge of market claim costs. Figure 3 provides several meaningful insights for the 1,250-life issuer.
1. As mentioned, despite knowing market average claims by member ahead of time (though not knowing a priori which members will enroll in each plan), 50% of our simulations result in post-risk adjustment profits of less than our 2% pricing target (anything to the left of the red dashed bar in Figure 3).
2. The spread of simulations suggests risk adjustment is inaccurate at estimating true plan liabilities, which can be more detrimental to smaller health plans that rely on greater stability. A large plan’s non-risk adjusted experience has greater natural stability, which is simply due to lesser statistical variation.
3. Risk adjustment may create difficulties predicting final pretax profit. To illustrate:
- Over one-third of simulations shift from profitable before risk adjustment (i.e., above 0% profit) to unprofitable after risk adjustment, or vice versa. Roughly half switch in one direction, and half in the other.
- Surprisingly, nearly 30% more either receive a risk adjustment transfer even if profitable prior to the transfer or pay into the program while already in a loss position. About one-third of the time, an issuer will experience a greater loss.
- About half of risk transfers amounts fall between +/-6% of premium, which means half are outside these bounds.
4. The fairly even distribution of individually simulated outcomes around priced-for profit explains the similarity between the average profit distributions in Figures 1 and 2 for the 1,250-life issuer. Risk adjustment’s “hits” and “misses” seem to reasonably offset in total—even though any one carrier in any one circumstance can experience significant over- or under-compensation. The simulations offset to such a degree that the average distribution of profit before and after risk adjustment is not meaningfully different, as noted earlier.
Similar to the concept of balancing imperfections over 10,000 scenarios for the smallest carrier, the same phenomenon happens as issuer size increases. The graph in Figure 4 displays simulated profit results for both the 7,500-life and 25,000-life issuers. We did not alter the scale in Figure 4 to better frame the differences in profit variability between various graphs.
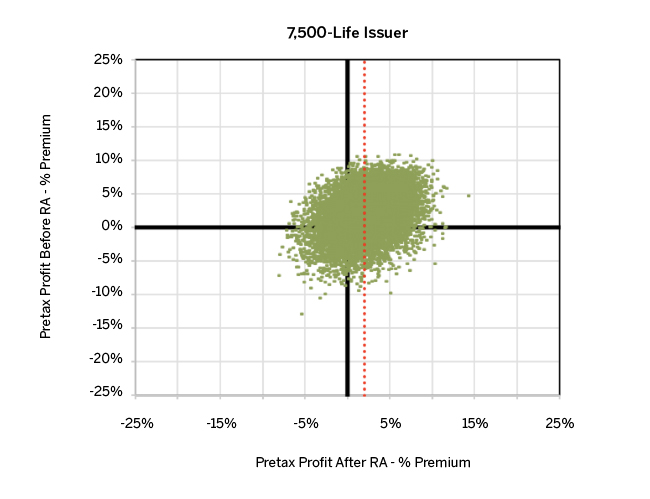
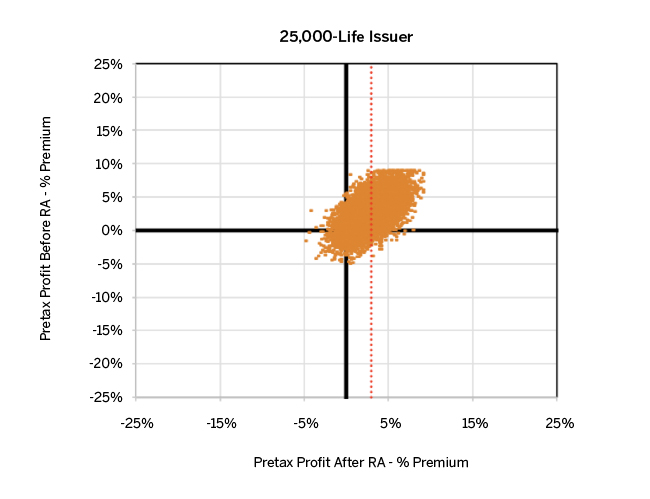
Figure 4 reveals a dramatic reduction in profit volatility for the 7,500-life issuer both before and after risk adjustment compared with the 1,250-life issuer, implying that a rather modest increase in membership can stabilize pretax profit quickly (risk-adjusted or not). The compression continues further for the 25,000-life issuer. Note, however, compression occurs because of plan size—not better performance of the risk transfer algorithm. Still, larger issuers experience a much narrower range of profit outcomes, as higher enrollee counts increase the probability of experiencing offsetting over- and under-compensation within a simulation. Figure 10 in the Appendix depicts a similar graph, with all issuer sizes and simulations to demonstrate how reductions in volatility scale with the size of the health plan. This scaling can be alternatively presented by the range of risk transfers for all 10,000 simulations for each issuer, as shown in the graph in Figure 5.
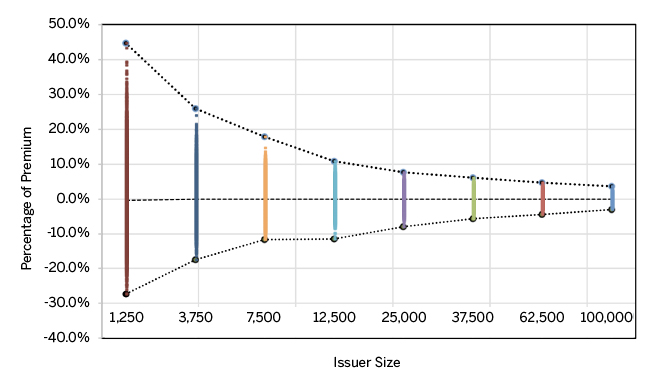
Figure 5 illustrates risk transfer results for health plans with a small relative market share are far more volatile than plans with larger shares. The pattern of transfer volatility further corroborates the compression in post-risk adjustment profit in Figure 4. We present several statistics related to risk transfers on a per member per month (PMPM) basis in Figure 11 of the Appendix.
These levels of unpredictability will be somewhat lessened in reality if an issuer has an established experience base from year to year to help estimate claim costs and transfer direction and magnitudes. Such stability of the experience could further insulate the health plan from the unknowns inherent in new enrollees. More research should be done on the progression of profitability over time to uncover these effects.
What is being done to address concerns about risk adjustment performance?
Over the past year, proposals have emerged across various forums to improve the risk adjustment program and ultimately reduce financial volatility.5,6 We briefly address the main concepts behind two types of proposals as they relate to the small health plan — changes to the application of the risk adjustment program and general enhancements to the risk score algorithm.
Changes to the application of the risk adjustment program
Risk transfer payment cap
We leverage our simulation model to estimate high-level outcomes introduced by capping risk transfers, selecting 2% of premium as the threshold given its prominence in recent discussions. We model two types of transfer caps—one affecting only risk transfer payments and another applying to both payments and receipts. We only summarize metrics associated directly with the cap itself. However, we appreciate the technical challenges associated with implementation (such as how to fund the transfer shortfall, how to incentivize issuers to improve patient outcomes, and how MLR rebates may be affected, among others).
We feel it is important to underscore that our theoretical modeling approach does not contemplate several nonstatistical sources of variation that are inherently part of the individual ACA insurance market, especially the availability of richer plan designs, selection and the potential effects from mis-pricing, risk adjustment data submission issues, or the dramatic morbidity shifts in 2014 relative to the pre-ACA, fully underwritten market reflected in our starting data. As such, the proportion of risk transfers relative to total market premium in our results is generally muted compared with the actual 2014 results. For instance, while total transfers represented an average of 10% of individual market premium in 2014, our modeling produces an average value of 1.1% of premium (with a high simulation of almost 3% of premium).
The values produced by our model are not unique relative to the 2014 transfer results even if not necessarily representative of most states’ individual outcomes. Our model’s lower variability in the risk transfers acts to dampen any impacts from a transfer cap. Meaning, the transfer cap effects presented in this section may be smaller than the 2014 market would have experienced. Though less impactful, we believe our model represents the direction risk transfers will move over time. We present several summary statistics for a cap on payments, a cap on collections, and a two-way cap in Figure 12 in the Appendix.
-
One-way cap on payments only: Under this scenario, we truncate risk transfers at 2% of the issuer’s premium when that issuer owes more than 2% of its premium to the risk adjustment program. Those owed a risk transfer are not capped, meaning all of the amount capped would require additional funding outside the risk adjustment program. At least one issuer experiences a payment cap in almost 90% of simulations. The average required funding amount to implement this type of one-way cap is equivalent to roughly 10% of the total annual risk transfer dollars changing hands for those simulations. This number, while not insignificant, is muted because smaller issuers have a higher chance of being capped, and they represent a relatively small portion of total market transfers. On average, a one-way cap should reduce profit volatility more as size declines. As an example, over 80% of the 1,250-life issuer’s simulations requiring a risk adjustment payment are capped, representing an average excess of 6% of premium over these scenarios. These two figures reduce to approximately 20% and 0.75%, respectively, for the 37,500-life plan.
There is a measure of volatility affecting transfer caps, as with risk transfers. While the average required funding is around 10% of total annual transfers for capped simulations, about 15% of them fall above 20% of annual transfers—scenarios that, if occurring, may be difficult to address with limited market disruptions. Additionally, if a cap is implemented in a revenue-neutral fashion across participating health plans, the smaller issuers (although benefiting more than any issuer size, on average) will experience another source of transfer movement for the 60% of simulations that are not capped. - Two-way cap on payments and receipts: For this scenario, we truncate all risk transfer payments and receipts greater than 2% of the carrier’s premium to exactly 2% of premium. This means some of the capped amount on payments would be offset by the cap on receipts. Nearly every one of the simulations is impacted by some amount under a two-way cap scenario, with an average amount capped relative to total risk transfers almost double the one-way cap. There are many different ways to analyze a two-way cap, but given the symmetrical nature of transfer payments and receipts perhaps the most telling statistic is that the average value of the cap over all issuers and scenarios is virtually zero. Meaning, over the long term, an issuer will experience roughly offsetting caps on payments and receipts if it attracts a new random mix of enrollees each year. It appears a two-way cap would evenly compress profit volatility for all issuers to a narrow range, though, perhaps even more at the expense of the main tenets of the risk adjustment program compared with a one-way transfer cap. However this compression would not necessarily ensure a zero-sum game in any given year across issuers or even across multiple years after implementation.
Interestingly, the relatively muted impacts presented above suggest there may be additional, more exaggerated, or different sources of variation in risk transfers in the actual marketplace—which would likely affect smaller issuers more profoundly than larger issuers. Whether examining the merits of a one-way or a two-way cap, both the cap’s size relative to market risk transfers and the potential volatility introduced would need to be factored into the equation when considering the potential funding mechanisms.
High-cost enrollees
Like most risk adjustment models, the U.S. Department of Health and Human Services hierarchical condition categories (HHS-HCC) model under-predicts plan liabilities for high-cost members. To address this deficiency, CMS has proposed a pool for high-cost members whereby total annual claims for each member over a certain threshold would be removed from the risk model calibration and funded through a different means.7
This idea will have considerable interplay with the existing commercial reinsurance marketplace. The status quo for small issuers would remain largely unchanged, except, perhaps, for any changes to existing reinsurance contracts to avoid duplicative coverage with the federal threshold and the associated expense savings. However, “reinsuring” all members in the market could provide value for larger health plans (whose size has allowed them to historically forgo reinsurance protection) through a “zero-cost” benefit. States also have the option of implementing their own reinsurance programs, providing a sanctioned method for shielding health plans from extreme loss.
Unless the attachment point is low enough, this proposal would probably not meaningfully limit the volatility experienced by small issuers beyond the benefits already realized through commercial reinsurance contracts.
Regional risk adjustment
Some issuers believe risk adjustment is predisposed to unfavorably impact smaller rural or regional plans, suggesting differences in provider coding patterns, the lack of centers of excellence, and better than average morbidity are obstacles for these issuers when compared with a statewide risk pool. Because the risk transfer calculation is performed at the state level, it is possible for a plan to experience selection within their region but also to be a contributor to the program if its risk relative to the state average is low enough. At its core, there is a concern regional players will need to raise premiums simply to subsidize the risk that exists in urban areas. Ultimately, the decision of which populations should be included in a given risk adjustment pool involves public policy considerations as well as actuarial considerations. Here we address only the latter.
Although current regulations constrain risk adjustment to a statewide calculation, what would happen to transfer volatility if CMS administered the program as revenue-neutral on a regional basis within each state? While more work is needed to understand second-order effects, our modeling suggests the program change would reduce volatility for regional issuers and increase it for larger, statewide players. For example, a smaller plan serving 10% of the statewide market but 40% of any one regional market, and that is one-quarter the size of the state, experiences a modeled decrease in the standard deviation of profit of approximately 19%. A similar, but opposite, effect occurs for larger plans at the regional level.
Our analysis of regional risk adjustment merits the following qualifications:
- Most of the attention related to regional risk adjustment is focused on larger, statewide issuers. However, smaller plans selling across the entire state or in several rating regions will experience the increased volatility associated with a shrinking risk adjustment membership base.
- While larger issuers will almost certainly experience higher volatility within each region, they will still benefit to a degree from combining results across multiple regions. This “benefit” would vary based on how the issuer’s population was distributed among regions, and it is not apparent if the large issuer would experience less volatility in total compared with a statewide calculation. Such an analysis lies beyond the scope of this paper.
- We are not suggesting total or average profitability changes for any plan, especially for larger carriers when summing the independent loss/gains across multiple regions. Rather, we stress that the deviation of profit is tied to both the relative issuer size and the absolute number of members the issuer covers.
Enhancements to the risk score algorithm
Prescription drug data
Assuming certain challenges are adequately addressed, prescription drug data could be incorporated into the risk adjustment model as soon as the 2018 plan year. Without additional analysis, it is uncertain whether this enhancement will reduce financial volatility. Two items for consideration include:
- The lack of pharmacy data in the model has solidified drug claims as a key indicator of coding improvement opportunities. It seems likely this addition into the model will help further equalize the risk adjustment playing field over time. Presently, small issuers face the difficult decision of either falling behind the coding intensity curve or investing significantly in coding efforts by partnering with outside vendors and consultants.
- Such significant changes to the model could create challenges in predicting the initial impacts, and they will very likely lead to larger issuers shifting strategies toward optimal prescribing patterns.
Partial-year enrollment
The 2014 transfer results revealed a weakness in risk adjustment’s ability to accurately model the true risk of partial-year enrollees for new issuers or those experiencing rapid midyear growth—either from typical small group turnover and purchasing patterns or from plans attracting a disproportionate number of special enrollment period members.8 The episodic nature of many medical cases certainly creates logistical difficulties in capturing HCC diagnoses for members moving to a new issuer midyear, which becomes harder to rectify the later in the year an insured switches coverage. Even those members with a controlled chronic illness may not present an opportunity for risk adjustment compensation if any medical treatment occurred during enrollment with another health plan. Partial-year enrollees may also incur costs for acute conditions that would be under-compensated compared with those members in-force a larger portion of the year.
CMS believes separating the risk adjustment models by enrollment duration would provide the greatest level of predictive accuracy and would most effectively capture the differing levels of relative cost between acute and chronic conditions.9 There may also be an opportunity to mitigate some of the unwanted side effects by folding pharmacy data into the HHS-HCC algorithm, which can identify members with HCCs more quickly. Regardless of the path, a balance must be struck between the increased modeling complexity and the benefits gained from reducing a real obstacle for new market entrants and fast-growing issuers.
Final thoughts
Risk adjustment in the commercial market has been specifically designed to transfer funds from plans with a lower average health status to plans with a higher health status,10 and recent studies have suggested this goal was realized in 2014. CMS did not initially intend for risk adjustment to completely offset a health plan’s financial volatility; still, there appear to be opportunities to address stability and support long-term marketplace competition.
While savvy insurers aim to understand their enrollee risk over time, membership churn will always introduce “unknowns” and, therefore, contribute a source of instability—particularly for small health plans. Several sources of turnover will continue to inhibit complete clarity into a plan’s risk profile for a given year, including movements of members into and out of the small group market, members entering and leaving the Medicaid space, and consumers annually purchasing the second-lowest-cost silver plan.
In terms of competition, the current risk adjustment program imposes a real barrier to entry for the ambitious start-up health plan or even for an established player looking to expand into additional states or markets. Whether health plans realize it or not, profit variability is inexorably linked to plan size, making growth an important initiative to avoid financial volatility. Grow too quickly, though, and an issuer will face pressure on capital resources and strain in certain operational areas. Health plans seem to be stuck choosing between rapid and measured growth—each one posing its own set of risks. However, issuers that manage to grow their membership levels at the right pace can quickly realize more stable ranges of profit outcomes.
In this paper, we have highlighted shortcomings in the risk adjustment program’s ability to effectively mitigate risk variation for which a smaller health plan may not have a reliable way to counteract. To say unequivocally, though, that risk adjustment disadvantages the smaller carrier is a bit simplistic and requires proper context of the program goals and known performance. Even before passage of the ACA, smaller health plans have faced unique challenges in managing risk and controlling unpredictability. Our analysis suggests, absent any changes, such challenges will likely continue.
Methodology and key assumptions
We premise this analysis on the concept of “perfect” market knowledge in a single year of pricing. We assume all issuers enter the ACA market for the first time and, therefore, do not have a prior block of ACA-specific experience. We grant every health plan full access to the future claim costs of those members who will purchase an individual medical plan. Even so, an issuer does not know in advance which members it will enroll and, therefore, only incorporates market average information into its pricing. Additionally, we assume equivalence of service areas, networks, discount levels, and, by extension, premium rates. Taken together, we create a random environment—unbiased by mis-pricing, positive or adverse selection, and competitive pressures—designed to isolate one year of risk adjustment transfer impacts.
We begin our analysis with the Truven Health Analytics 2013 MarketScan Commercial Claims and Encounters (MarketScan) database. This database reflects nationwide healthcare experience for insured employees, spouses, and dependents, as collected from approximately 100 different insurance companies, Blue Cross Blue Shield plans, and third-party administrators. We select only members with both medical and prescription drug coverage and with robust coding of diagnoses throughout their claim records. Even after applying these filters, approximately 13 million unique members remain in the starting data set.
We then extract a stratified random 250,000-member sample, representing a theoretical individual ACA market in a sufficiently sized state. We stratify by age when sampling to target a specific demographic distribution representative of the current individual ACA market (as reported in publicly available ACA exchange data sources). The average age of the members underlying this analysis is approximately 43 years. We perform this sampling process only once and use the results for all subsequent modeling.
All health plans in our theoretical ACA market offer a single, silver level deductible/coinsurance plan with the same set of benefits across issuers. This benefit plan conforms to the requirements on the final 2017 Federal Actuarial Value Calculator. We do not model cost-sharing reduction (CSR) variants.
We develop a paid claim estimate for each member by trending their allowed medical and prescription drug claims to 2017 and adjudicating to the cost-sharing parameters of our silver plan. We do not subject preventive service claim lines to member cost-sharing. We calculate two paid claim estimates for each issuer—one unmodified after adjudication and one with a $300,000 annual member stop-loss deductible representing commercial reinsurance coverage. We assume all services rendered represent valid essential health benefits (EHBs), as mandated by our “state.” We do not price risk adjustment transfers into our manual premium rate, given no one issuer has prior ACA experience nor a basis to assume whether it will attract risk differently than the market average.
We produce a final manual premium rate for the 2017 market from the total modeled gross paid claims PMPM and an overall retention assumption of 20%. We display the build-up of the overall retention assumption in the table in Figure 6.
| Figure 6: Market-wide Pricing Assumptions | |
| Assumption | % of Premium |
| General Administration and Commissions | 11.50% |
| Quality Improvement | 0.80% |
| Premium Tax | 1.00% |
| Composite Exchange Fee | 3.15% |
| Health Insurer Provider Fee | 0.50% |
| PCORI and RA Administration | 0.05% |
| Pretax Profit* | 3.00% |
| * Lower for issuers opting to purchase commercial reinsurance coverage | |
For those issuers purchasing commercial reinsurance, we do not vary the manual premium rate from other issuers opting out of such coverage. This implicitly means:
- The cost of the reinsurance coverage, to start, reflects the average expected rate of claims across the entire market over the $300,000 stop-loss deductible, or roughly 3.75% of premium.
- The additional amount needed to cover the reinsurer’s required profit reduces the priced-for profit target—in other words, if an issuer prefers stability, we require them to accept a lower expected pretax margin. For this analysis, the margin for reinsured issuers is approximately 2%. While modeling commercial reinsurance lowers average profit below the 3% presented in Figure 6, it mirrors the strategies employed by many smaller health plans in the current market.
We produce a market-wide base premium rate by applying the market’s composite age rating factor to the manual premium. Because there is only one silver plan in the entire market, we ignore the impact of plan factors. For simplicity, we also ignore geography, tobacco use, and rating restrictions imposed on issuers for families with more than three children (which means member months and billable member months are equivalent).
We append commercial HCCs to each member using our internal implementation of the CMS HHS-Developed Risk Adjustment Model Algorithm “Do It Yourself” Software (CMS DIY Tool), released October 19, 2015. While the stock CMS model contains risk score coefficients for the 2014 and 2015 plan years, we replaced all age/gender and condition coefficients with the recently released and finalized 2017 parameters. We use the HCC information to calculate the member- and market-level risk scores in the risk transfer equation. Because we select a single marketwide silver plan and ignore both CSR variations and geographic differences, we are also able to bypass the impacts of actuarial value, induced demand, and geographic costs in the final risk transfer calculation. The state average premium is equivalent to the market manual premium rate PMPM.
Next, we simulate a sample market by randomly assigning members from our 250,000-member data set to one of eight issuers based on the distributions in the graph in Figure 7.

We repeat the reassignment process randomly until we arrive at 10,000 independent market simulations. Because members in our starting pool retain their allowed claim costs no matter which issuer they end up with, we implicitly assume a single provider discount rate in the market.
We record the premium, claim, and risk transfer results by issuer for each of the 10,000 simulations. We impose a $300,000 cap on annual paid claims per member for those health plans with no more than 12,500 members (5% market share), assuming most small issuers insulate themselves from catastrophic claims and random fluctuation via commercial reinsurance contracts. As mentioned above, we make the simplifying assumption reinsurance premiums will be completely offset by average reinsurance payments received for claims over $300,000 except for the margin built into the contract (which reduces the issuer’s priced-for profit and keeps the rates constant with other issuers not purchasing reinsurance).
We model pretax profit by issuer, after removing administration expenses and taxes and fees and then calculating a one-year MLR rebate, including applicable credibility adjustments based on issuer size and our plan’s $2,000 deductible. As a final step, we summarize the results for each simulation and calculate various profit/loss metrics by issuer size.
The graphs in Figures 1 and 2 above display noticeable “spikes” in number of simulations for certain issuer sizes at very specific profit levels, which is the natural consequence of the MLR rebate program. The positioning of these profit spikes on the graphs is predictable, though, as issuers with extremely low claims will most often realize pretax profit equivalent to:
- The priced-for profit
- Plus the value of the credibility adjustment (approximately 7.8% in the case of our 1,250-life issuer)
- Plus the difference between the 80% MLR target and the adjusted loss ratio, after factoring in allowable quality improvement and tax/fee credits
- Less any additional administrative expenses for those issuers opting for commercial reinsurance protection
Not all issuers are capped at this profit level, as evidenced by the continuing profit tail for the smallest issuers. Profit levels can be augmented when high gross claims are offset by commercial reinsurance. Because the MLR rebate formula uses gross claims in the numerator, an issuer might have an adjusted MLR well above 80% but have a true loss ratio much lower (and thus can retain that favorable experience as margin). We include two distinct examples—one simulation with a rebate payment and a separate simulation without—in Figure 13 in the Appendix, demonstrating the circumstances in which high margin manifests itself for the 1,250-life issuer. Note, larger issuers in our simulation rarely pay rebates, and the probability is inversely related to plan size. For instance, the 1,250-life issuer pays rebates without applying risk transfers and after applying transfers in about 12% and 7.5%, respectively, of our simulations.
We performed the following reasonability checks on our model:
- We compared key metrics (i.e., premium, claims PMPM, average age and the implied allowable rating factor, risk scores, overall HCC prevalence rates) from our sample data set with known ACA market values from several sources. All of our key metrics are reasonable given our market knowledge and the nature of our starting data set.
- We performed our simulations without the impact of commercial reinsurance to ensure all market statistics behaved as expected. We include a graph similar to Figure 3 above, except without commercial reinsurance, in Figure 14 in the Appendix.
- We recognize that not all expenses should be treated as variable, so we tested the outcomes of the simulation with 100% variable and a portion of general administrative expenses fixed. The results were not meaningfully different.
- We repeated the 10,000 market simulation exercise on several distinct starting populations to ensure the results were not unique to our selected 250,000-member sample.
Limitations
The following limitations should be considered when reviewing the results of our study.
We assume perfect knowledge for all market issuers in the pricing process and no differentiation in plans, service area, or premium rates by issuer. As such, we create a truly random environment where prospective members are not incentivized to select one plan over another. In practice, however, many subtleties dictate which health plan a member selects, including brand recognition, price, benefit offerings, and network, among others. Also, larger issuers typically have more market knowledge over the long term, creating an advantage in rate setting over smaller health plans. By keeping the analysis random and giving all issuers in the simulation a “fair” chance of attracting any one member, we make a trade-off between depicting a truer representation of the current ACA market and the raw probabilistic patterns underlying the information.
We look at all results over a single plan year and track the results for only that year. Over time, even without full market knowledge, issuers will adjust strategies, rates, and other levers to try to more optimally position themselves. Additionally, with a 100% random analysis over multiple years, all issuers will still tend to regress toward a mean profitability level—some quicker than others (although the one-sided nature of the MLR rebate formula can distort this somewhat). We do not model issuer sustainability or ruin in this analysis.
The following is a list of simplifying assumptions in the analysis that, given the manner in which we set pricing and run the simulations, we believe will not have a material impact on the patterns we present. Should we model a more realistic market, we would need to revisit all these assumptions.
- Our starting data set is heavily comprised of members on large group plans and is not necessarily representative of the individual ACA insurance market. While we attempt to control for age, we did not adjust the starting sample for all known and relevant nuances of the current individual market.
- All polices are effective January 1, 2017, but not all members have a full 12 months of enrollment.
- Our experienced member months per enrollee are based on patterns in large group data and not on the specific lapse patterns many issuers have experienced in the individual ACA market, which are due to open enrollment and special enrollment periods.
- Ages in the data set reflect the member’s 2017 age (i.e., we do increase member ages beyond those implied by the MarketScan enrollment data). We calculate the allowable rating factor in the risk transfer equation and the demographic calibration factor in our premium rating using these ages and the ACA federal age curve.
- We ignore regional dynamics, instead opting for a simulated state with one rating region and all issuers selling in every county within that region.
- It is likely the disease prevalence rates in our data are different (either higher or lower) than the current individual ACA market. Actual HHS-HCC prevalence rates reflect a guaranteed issue environment and the migration of previously uninsured individuals into the insurance market—neither of which is reflected in the starting MarketScan data. Further, because we use only one random sample from our starting data, there is no guarantee the conditions in this sample will accurately represent the prevalence rates underlying the overall data.
- The benefit plans associated with MarketScan will not conform to all ACA requirements. Most notably, the data will likely contain many plans that do not cover a small portion of now mandated EHBs.
- Our analysis is limited to a single plan design. Results could vary for other plan designs.
- Every member in the starting population purchases an individual policy (i.e., we ignore family structures).
- All issuers maintain the same level of medical coding intensity.
- We apply commercial reinsurance premium and claim stop-loss to the four smallest issuers only.
- We calculate retention as a percentage of premium for all expenses, taxes, and fees.
- We use only a single randomly-generated member sample of 250,000. It is possible for the results to vary somewhat for other randomized samples, though we note above that the patterns of outcomes demonstrate consistency for the several samples we tested.
When developing the market premium rates, we apply a constant retention assumption for all issuers regardless of size. Larger issuers should have an expense advantage in practice beyond the reinsurance differences we modeled. However, recognizing this additional advantage would have increased the variability in the analysis and created unnecessary complications, jeopardizing the random nature of the study.
Our results represent one pool of individuals, one benefit plan, and one set of assumptions, which are not necessarily representative of any particular health plan. Our results may be different if any of these assumptions were materially altered.
Lastly, at any time, the results we present could change depending on the shifting legislative environment. Since full implementation of the ACA, aspects of the risk adjustment program alone have been modified several times. Should any salient feature of the ACA change, our conclusions may no longer apply.
Appendix
The following tables provide additional details and support the overall analysis. This information is not exhaustive.
Figure 8 displays high level experience statistics from Figures 1 and 2 above.
| Figure 8: Simulation Summary Statistics | |||||
| Issuer Size | 100,000 | 37,500 | 7,500 | 3,750 | 1,250 |
|
Average Across All Simulations, PMPM
|
|||||
| Premium | $611.54 | $611.57 | $611.56 | $611.52 | $611.57 |
| Allowed Claims | $633.84 | $633.95 | $634.11 | $633.85 | $633.73 |
| Raw Paid Claims | $489.18 | $489.28 | $489.45 | $489.18 | $489.11 |
| Net Paid Claims* | $489.18 | $489.28 | $472.06 | $472.07 | $471.98 |
|
Standard Deviation Across All Simulations, PMPM
|
|||||
| Premium | $0.65 | $1.27 | $3.01 | $4.33 | $7.47 |
| Allowed Claims | $5.78 | $11.23 | $27.11 | $38.00 | $66.88 |
| Raw Paid Claims | $5.66 | $11.01 | $26.58 | $37.28 | $65.60 |
| Net Paid Claims* | $5.66 | $11.01 | $20.95 | $29.78 | $52.33 |
| *Commercial reinsurance caps annual member claims for simulated issuers below 12,500 lives at $300,000 | |||||
Figure 9 displays several profitability statistics from Figures 1 and 2 above.
| Figure 9: Summarized Pretax Profitability Statistics | |||||
| Issuer Size | 100,000 | 37,500 | 7,500 | 3,750 | 1,250 |
|
Excluding Risk Adjustment
|
|||||
| Minimum | -1.1% | -4.4% | -12.9% | -17.9% | -34.8% |
| Maximum | 6.4% | 8.9% | 10.9% | 14.1% | 21.6% |
| Average | 3.0% | 3.0% | 2.0% | 1.9% | 1.6% |
| Standard Deviation | 0.9% | 1.8% | 3.3% | 4.6% | 7.8% |
| Probability of Positive Margin | 100.0% | 95.0% | 73.0% | 67.2% | 61.1% |
|
Including Risk Adjustment
|
|||||
| Minimum | 0.2% | -2.7% | -8.2% | -14.2% | -26.6% |
| Maximum | 6.1% | 8.9% | 14.2% | 16.4% | 30.0% |
| Average* | 3.0% | 3.0% | 2.1% | 2.0% | 1.8% |
| Standard Deviation | 0.8% | 1.5% | 3.0% | 4.2% | 7.1% |
| Probability of Positive Margin | 100.0% | 97.5% | 75.1% | 68.3% | 60.3% |
| *Carriers below 12,500 lives price to a lower profit after accounting for commercial reinsurance premium | |||||
Figure 10 displays the relationship of pre- and post-risk adjustment profit for all issuer sizes, stacked to highlight the reduction in profit volatility as membership increases. The largest issuers are in the foreground. Volatility quickly compresses as market share increases. However, the volatility for any carrier size maintains the same oblong (although continuously shrinking) shape, implying risk adjustment compression is due to size and not model performance or “accuracy.”
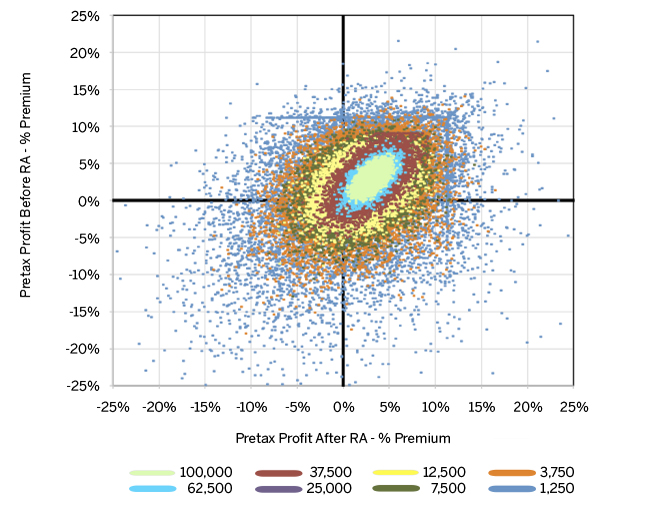
Figure 11 displays several PMPM summary statistics related to risk transfer payments from Figure 5 above.
| Figure 11: Risk Transfer Summary Statistics, PMPM | |||||
| Issuer Size | 100,000 | 37,500 | 7,500 | 3,750 | 1,250 |
| Minimum | -$18.74 | -$34.38 | -$71.21 | -$106.97 | -$171.66 |
| Maximum | $22.05 | $37.55 | $110.00 | $156.19 | $275.46 |
| Median | -$0.06 | -$0.05 | -$0.32 | -$0.72 | -$3.19 |
| Average | -$0.06 | $0.04 | $0.20 | $0.31 | -$0.08 |
| Standard Deviation | $4.85 | $9.45 | $22.84 | $32.16 | $56.06 |
Figure 12 displays several summary statistics related to a risk transfer payment cap at 2% of premium. Note, that the average values in this table are based on only the 10,000 simulations and only those capped. Further, “% of Risk Transfers” refers to a comparison with the absolute value of transfers (i.e., the total dollars changing hands).
| Figure 12: Risk Transfer Cap Summary Statistics | ||||||
|
One-Way Cap on Payments
|
||||||
| Issuer Size | 100,000 | 37,500 | 7,500 | 3,750 | 1,250 | Total Market |
| Total Simulations Capped | 0.5% | 9.7% | 30.2% | 35.7% | 43.7% | 88.2% |
| Average Cap Value for Transfer Payment Simulations - % of Premium | 0.25% | 0.72% | 2.23% | 3.37% | 6.14% | 0.11% |
| Average Cap Value for Transfer Payment Simulations - % of Risk Transfers | 0.05% | 1.03% | 2.00% | 1.79% | 1.33% | 10.0% |
| Max Cap Value - PMPM | $6.50 | $22.13 | $58.93 | $94.71 | $159.11 | $4.06 |
| Max Cap Value - % of Premium | 1.1% | 3.6% | 9.6% | 15.5% | 25.4% | 0.66% |
| Max Cap Value - % of Risk Transfers | 15.8% | 29.4% | 35.7% | 28.7% | 24.0% | 41.2% |
|
One-Way Cap on Collections
|
||||||
| Issuer Size | 100,000 | 37,500 | 7,500 | 3,750 | 1,250 | Total Market |
| Total Simulations Capped | 0.5% | 9.9% | 29.3% | 34.1% | 38.9% | 86.2% |
| Average Cap Value for Transfer Payment Simulations - % of Premium | -0.27% | -0.74% | -2.46% | -3.76% | -7.09% | -0.12% |
| Average Cap Value for Transfer Payment Simulations - % of Risk Transfers | -0.05% | -1.10% | -2.18% | -1.94% | -1.39% | -10.8% |
| Max Cap Value - PMPM | -$9.82 | -$25.31 | -$97.70 | -$144.12 | -$263.14 | -$4.49 |
| Max Cap Value - % of Premium | -1.6% | -4.1% | -15.9% | -23.9% | -42.7% | -0.73% |
| Max Cap Value - % of Risk Transfers | -22.1% | -29.2% | -36.3% | -31.8% | -21.6% | -40.0% |
|
Two-Way Transfer Cap
|
||||||
| Issuer Size | 100,000 | 37,500 | 7,500 | 3,750 | 1,250 | Total Market |
| Total Simulations Capped | 1.0% | 19.6% | 59.5% | 69.7% | 82.6% | 99.4% |
| Average Cap Value for Transfer Payment Simulations - % of Premium | 0.00% | -0.02% | -0.08% | -0.12% | -0.09% | -0.01% |
| Average Cap Value for Transfer Payment Simulations - % of Risk Transfers | 0.1% | 1.9% | 3.7% | 3.3% | 2.4% | 18.7% |
| Max Cap Abs. Value - % of Risk Transfers | 22.1% | 29.4% | 36.3% | 31.8% | 24.0% | 54.9% |
Figure 13 displays how an issuer can retain profit beyond what MLR rebates would seemingly allow. High margin situations arise from the disparity of gross and net claim costs caused by the interplay of claim experience, risk adjustment, and commercial reinsurance recoveries. The two examples represent distinct simulations from the 1,250-life issuer—one where an MLR rebate was paid and one where a rebate was not paid.
| Figure 13: Depiction of Distinct High Margin Simulations, 1,250-Life Issuer | ||
| Metric | Simulation Without MLR Rebates | Simulation With MLR Rebates |
| Premium PMPM | $615.56 | $606.72 |
| Gross Paid Claims PMPM | $507.74 | $426.48 |
| Net Paid Claims PMPM* | $449.01 | $409.89 |
| Risk Transfer Receipt PMPM | $87.03 | $75.58 |
| MLR | 80.3% | 69.3% |
| Rebate Paid PMPM | $0.00 | $61.81 |
| Expenses | $127.78 | $125.94 |
| Realized Margin | 20.4% | 14.0% |
| *After commercial reinsurance with a $300,000 stop-loss deductible. | ||
Figure 14 displays the relationship between pre- and post-risk adjusted profit without consideration for commercial reinsurance for the 1,250-life issuer. Because gross and net claims are equivalent in this case, all profit outside a certain threshold is capped and paid out as MLR rebates. The dispersion in the lower left quadrant is more pronounced than in Figure 3 above because of those simulations now bearing the full impact of the catastrophic claims above $300,000.
The authors would like to thank Hans Leida, Jim O’Connor, and Scott Weltz for their contribution as peer reviewers of this article.
1Perlman, D. and Liner, D. (February 2016). February 19, 2016, Financial analysis of ACA health plan issuers. Retrieved April 11, 2016, from /-/media/Milliman/importedfiles/uploadedFiles/insight/2016/2180hdp_20160224.ashx
2American Academy of Actuaries (April 2016). Insights on the ACA Risk Adjustment Program. Retrieved April 11, 2016 from http://actuary.org/files/imce/Insights_on_the_ACA_Risk_Adjustment_Program.pdf
3Giesa, K. (March 2016). March 24, 2016, A Story in 4 Charts: Risk Adjustment in the Non-Group Market in 2014. Retrieved April 11, 2016, from http://health.oliverwyman.com/maximize-value/2016/02/a_story_in_four_char.html
4Centers for Medicare & Medicaid Services (March 2016). March 31, 2016, HHS-Operated Risk Adjustment Methodology Meeting Discussion Paper. Retrieved April 11, 2016, from https://www.cms.gov/CCIIO/Resources/Forms-Reports-and-Other-Resources/Downloads/RA-March-31-White-Paper-032416.pdf
5March 31, 2016, HHS-Operated Risk Adjustment Methodology Meeting Discussion Paper, ibid.
6Consumers for Health Options, Insurance Coverage in Exchanges in States (November 4, 2015). Technical Issues with Risk Adjustment and Risk Corridor Programs. Letter to U.S. Department of Health and Human Services Secretary Sylvia Burwell. Retrieved May 24, 2015, from http://nashco.org/wp-content/uploads/2015/11/CHOICES-White-Paper-on-Risk-Adjustment-Issues.pdf.
7March 31, 2016, HHS-Operated Risk Adjustment Methodology Meeting Discussion Paper, ibid., p.71.
8March 31, 2016, HHS-Operated Risk Adjustment Methodology Meeting Discussion Paper, ibid., p.35.
9March 31, 2016, HHS-Operated Risk Adjustment Methodology Meeting Discussion Paper, ibid., p.38.
10March 31, 2016, HHS-Operated Risk Adjustment Methodology Meeting Discussion Paper, ibid., p .6
About the Author(s)
Nicholas Krienke
Alan Vandagriff
Sizing up ACA risk adjustment volatility: How the interplay between risk adjustment and issuer size influences profitability under the ACA
This study explains how risk adjustment might influence profitability patterns in a typical year and whether those patterns change with the size of a health plan.